Kuzey doğrultusu, yön bulma ve seyrüsefer (navigasyon) problemlerinin çözümünde kullanılan doğal bir doğrultudur. Pratikte; ağaç yosunları, karınca yuvaları, mezar taşları, gölge çubuğu, analog saat ve güneş, kutup yıldızı, pusula gibi yöntem ve araçlar kullanılarak kuzey yönü tayin edilebilmektedir. Günümüzde ataletsel navigasyon sistemleri (INS) ve küresel navigasyon uydu sistemleri (GNSS) vasıtasıyla kuzey doğrultusu hassas bir şekilde belirlenebilmektedir.
Kuzey tayini, yeryüzünde iki noktayı birleştiren doğrultunun kuzey istikametinden olan açıklığı yani baş açısı veya azimut açısının belirlenmesi işlemidir. GPS/GNSS ile kuzey tayini için iki noktanın konumuna ihtiyaç vardır. Bu amaçla, öncelikle birinci nokta üzerinde TUSAGA-Aktif sistemiyle veya statik gözlem yapılarak konum hesaplanır. Daha sonra ikinci bir nokta seçilir ve benzer şekilde bu noktanın da konumu belirlenir. Her iki noktanın coğrafi koordinatları (enlem, boylam) kullanılarak ikinci temel ödev eşitlikleri ile veya bir noktaya merkezli toposentrik koordinatlardan (NED, ENU) yararla jeodezik azimut açısı hesaplanır. Jeodezik azimutun astronomik azimuta dönüştürülmesi için Laplace eşitliği uygulanır. Bunun için birinci noktada çekül sapması bileşenlerinin bilinmesi gerekmektedir. Çekül sapması bileşenleri uygun bir yer gravite alanı modelinden türetilebilir. Astronomik azimut belirlendikten sonra birinci nokta üzerine bir teodolit veya total station kurulur ve ikinci noktaya bakılarak yatay açı tablası sıfırlanır. Dürbün astronomik azimut açısı kadar döndürülerek gerçek kuzey istikameti bulunur.
Çekül Sapması:
Çekül sapması (θ), bir noktadaki gravite vektörü (g) ile aynı noktadaki belli bir elipsoit için elipsoit normali arasındaki açıdır.
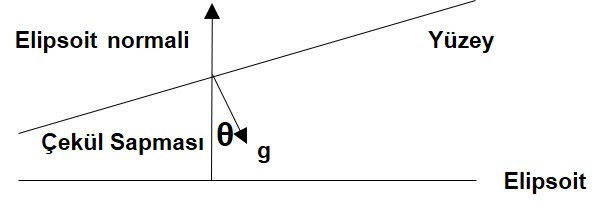
Vektörel bir büyüklük olan çekül sapması genelde birbirine dik iki bileşene ayrılır: pozitif yönü kuzey olan kuzey-güney bileşen (ξ) ve pozitif yönü doğu olan doğu-batı bileşeni (η). Çekül sapması rölatiftir. Eğer elipsoit değişirse, çekül sapması da değişir.
Bir noktanın astronomik enlem (Φ) ve boylamı (Λ) ile jeodezik enlem (φ) ve boylamı (λ) biliniyorsa, çekül sapması ve bileşenleri şu şekilde belirlenebilir:
ξ = Φ – φ,
η = (Λ – λ) * cos φ
θ = √(ξ2 + η2)
Çekül sapmasının herhangi bir α azimutu doğrultusundaki bileşeni:
ε = ξ * cos α + η * sin α
Yersel ölçmelerde, çekül sapmasının 3 temel kullanım alanı vardır. Astronomik koordinatlarla jeodezik koordinatlar arasında dönüşüm, Astronomik azimut ile jeodezik azimut arasında dönüşüm, Düşey ve yatay açıların sferoide indirgenmesi.
Azimut için Laplace Eşitliği:
Gözlemlenen Astronomik azimutun (A) jeodezik azimuta (α) çevrilmesinde veya tam tersi durumda çekül sapmasına ihtiyaç vardır.
α = A – (η * tan Φ) – (ξ * sin α - η * cos α) cot z
“z”; gözlemleyen ve gözlemlenen istasyonlar arasındaki zenit açısıdır. Çoğu jeodezik ağ için, z değeri 90 dereceye çok yakındır. Eşitlik bu durumda Laplace düzeltmesine dönüşür:
α = A – (η * tan Φ)
α: Jeodezik azimut
ϕ: Jeodezik enlem